LIRIK LAGU : Contoh Soal Dimensi Tiga Dan Pembahasannya

Contoh Soal Dimensi Tiga dan Pembahasannya - Dalam pelajaran Matematika terdapat bahan mengenai dimensi tiga. Materi ini biasanya diajarkan pada tingkat Sekolah Menengah Atas (SMA) sederajat. Apa yang dimaksud dimensi tiga itu? Dimensi tiga ialah ilmu Matematika yang mempelajari wacana bidang, titik dan garis pada berdiri ruang serta bekerjasama pula dengan sudut dan jarak. Lantas bagaimana cara menuntaskan teladan saol dimensi tiga itu? Cara menuntaskan soal tersebut sanggup memakai rumus dimensi tiga yang terkait tergantung pada bentuk bangunnya.

Dimensi tiga dalam Matematika sanggup dibagi menjadi beberapa macam ibarat kubus, balok dan sebagainya. Dari sinilah sanggup kita ketahui bahwa rumus dimensi tiga yang dipakai tergantung pada bentuk bangunnya serta apa yang ditanyakan. Pada kesempatan kali ini saya akan membagikan beberapa teladan soal dimensi tiga dan pembahasannya. Untuk lebih jelasnya sanggup anda simak di bawah ini.

Contoh Soal Dimensi Tiga dan Pembahasannya

Mempelajari berdiri tiga dimensi memang sangatlah penting. Materi ini bahkan ikut andil dalam aneka macam tes baik itu UTS, UAS, sampai ujian nasional sekalipun. Sebelum membagikan beberapa teladan soal wacana dimensi tiga dan pembahasannya. Saya akan membagikan beberapa konsep rumus dimensi tiga. Agar anda lebih memahami lebih lanjut maka sanggup anda perhatikan konsep rumus di bawah ini: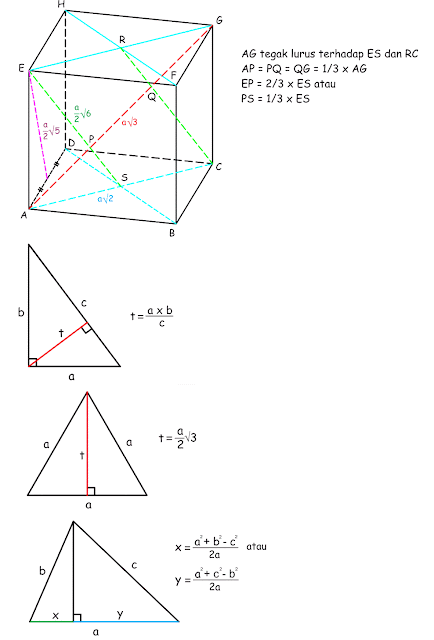

Konsep Rumus Dimensi Tiga Secara Umum

Baca juga : Sifat Sifat Operasi Bilangan Bulat Matematika Kelas 5 SD

Berdasarkan kurikulum 2013 kita sebagai siswa diharuskan untuk memahami rumus dimensi tiga dan harus sanggup mengerjakan teladan soal dimensi tiga dengan benar. Dari gambar diatas sanggup kita amati beberapa rumus dasar tiga dimensi. Lantas ibarat apa teladan soal tiga dimensi? silahkan simak klarifikasi saya di bawah ini.

Contoh Soal Dimensi Tiga

Setelah memahami wacana konsep rumus dimensi tiga di atas, selanjutnya saya akan membagikan beberapa teladan soal terkait rumus tersebut. Berikut teladan soal dan pembahasannya yaitu:

1. Sebuah kubus ABCD.EFGH mempunyai rusuk yang panjangnya 3a cm. Berapakah panjang garis pada ruas HB?

Pembahasan Contoh Soal Dimensi Tiga #1
Perhatikan gambar di bawah ini!

soal%2B11.jpg" imageanchor="1" style="margin-left: auto; margin-right: auto;">soal%2B11.jpg" title="Contoh Soal Dimensi Tiga dan Pembahasannya" />

Gambar Kubus ABCD.EFGH

Langkah pertama yang perlu dilakukan ialah mencari nilai DB melalui segitiga BAD siku siku di A. Untuk menentukannya sanggup memakai rumus pythagoras ibarat di bawah ini:

Setelah itu mencari nilai HB dengan memperhatikan segitiga HDB siku siku di D. Untuk menentukannya sanggup memakai rumus pythagoras ibarat di bawah ini:

Kaprikornus panjang garis HB ialah 3a√3 cm.

2. Sebuah kubus ABCD.EFGH mempunyai rusuk yang panjangnya 9 cm. Hitunglah jarak titik B menuju garis HC?

Pembahasan Contoh Soal Dimensi Tiga #2
Perhatikan gambar di bawah ini!

soal%2B2.jpg" imageanchor="1" style="margin-left: auto; margin-right: auto;">soal%2B2.jpg" title="Contoh Soal Dimensi Tiga dan Pembahasannya" />

Gambar Kubus ABCD.EFGH

Jarak dari titik B menuju garis HC sama halnya dengan jarak antara titik B menuju titik C. Dalam gambar diatas terdapat rusuk kubus yaitu BC dengan panjang 9 cm. Maka dari itu jarak titik B ke C panjangnya 9 cm.
Kaprikornus jarak antara titik B menuju garis HC ialah 9 cm.

3. Sebuah kubus ABCD.EFGH mempunyai rusuk yang panjangnya 8 cm. Hitunglah jarak titik B menuju garis EG?

Pembahasan Contoh Soal Dimensi Tiga #3
Perhatikan gambar di bawah ini!

soal%2B3.jpg" imageanchor="1" style="margin-left: auto; margin-right: auto;">soal%2B3.jpg" title="Contoh Soal Dimensi Tiga dan Pembahasannya" />

Gambar Kubus ABCD.EFGH

Jika ditarik garis ibarat gambar di atas, jarak titik B ke garis EG akan membentuk segitiga sama sisi yakni segitiga BEG, dimana setiap sisinya merupakan diagonal sisi kubus. Maka dari itu BE = GE = EB mempunyai panjang senilai 8√2 cm. Karena ditanyakan jarak B ke EG maka akan terbentuk titik O diantara garus EG. Dengan kata lain jarak B ke EG sama dengan jarak B ke O.

Baca juga : Rangkuman Materi Transformasi Geometri dan Rumus

Untuk memilih panjang garis BO sanggup memakai teorema phytagoras ibarat di bawah ini:

Kaprikornus jarak titik B menuju garis EG ialah 4√6 cm.

4. Sebuah kubus ABCD.EFGH mempunyai rusuk yang panjangnya 6 cm. Jika garis EH mempunyai titik tengah yang dinamakan titik P. Berapakan jarak titik P menuju garis AG?

Pembahasan Contoh Soal Dimensi Tiga #4
Perhatikan gambar di bawah ini!

soal%2B4.jpg" imageanchor="1" style="margin-left: auto; margin-right: auto;">soal%2B4.jpg" title="Contoh Soal Dimensi Tiga dan Pembahasannya" />

Gambar Kubus ABCD.EFGH

Jika setiap titik yang ditanyakan ditarik garis maka akan membentuk gambar ibarat di atas. Hal pertama yang perlu dilakukan ialah mencari nilai PG pada segitiga PHG. Untuk mencari nilai PG sanggup memakai rumus pythagoras ibarat di bawah ini:

Setelah diketahui panjang garis PG, kemudian mencari panjang OP dalam segitiga POG. Cara mencarinya hampir sama dengan langkah langkah di atas yaitu memakai konsep teorema pythagoras ibarat di bawah ini:

Kaprikornus jarak titik P menuju garis AG ialah 3√2 cm.

5. Sebuah kubus ABCD.EFGH mempunyai rusuk yang panjangnya 16 cm. Jika garis CG mempunyai titik tengah yang dinamakan titik M. Berapakan jarak titik M menuju garis HB?

Pembahasan Contoh Soal Dimensi Tiga #5
Perhatikan gambar di bawah ini!

soal%2B5.jpg" imageanchor="1" style="margin-left: auto; margin-right: auto;">soal%2B5.jpg" title="Contoh Soal Dimensi Tiga dan Pembahasannya" />

Gambar Kubus ABCD.EFGH

Jika setiap titik yang ditanyakan ditarik garis maka akan membentuk gambar ibarat di atas. Hal pertama yang perlu dilakukan ialah mencari nilai MB pada segitiga MCB. Untuk mencari nilai MB sanggup memakai rumus pythagoras ibarat di bawah ini:

Dalam gambar kubus di atas garis HB ialah diagonal kubus yang rumusnya s√3. Kaprikornus panjang HB = 16√3 cm. Untuk itulah panjang OB = 8√3 cm. Langkah selanjutnya ialah mencari panjang garis MO sehabis garis MB diketahui panjangnya. Untuk mencari panjang MO sanggup memakai prinsip teorema pythagoras ibarat di bawah ini:

Kaprikornus jarak titik M menuju garis HB ialah 8√2 cm.

Baca juga : Kesebangunan dan Kekongruenan Bangun Datar dalam Matematika

6. Sebuah kubus ABCD.EFGH mempunyai rusuk yang panjangnya 6 cm. Jika garis FG mempunyai titik tengah yang dinamakan titik P. Berapakan jarak titik P menuju garis BD?

Pembahasan Contoh Soal Dimensi Tiga #6
Perhatikan gambar di bawah ini!

soal%2B6.jpg" imageanchor="1" style="margin-left: auto; margin-right: auto;">soal%2B6.jpg" title="Contoh Soal Dimensi Tiga dan Pembahasannya" />

Gambar Kubus ABCD.EFGH

Jika setiap titik yang ditanyakan ditarik garis maka akan membentuk gambar ibarat di atas. Hal pertama yang perlu dilakukan ialah mencari nilai BP pada segitiga BFP. Untuk mencari nilai BP sanggup memakai rumus pythagoras ibarat di bawah ini:

Jika diagonal garis BC dibelah dua maka akan terbentuk titik tengah yang disimbolkan karakter O. Kemudian akan terbentuk segitiga DOP. Dari sinilah akan terdapat panjang garis OP = 6 cm dan DO = BP = 3√5 cm. Langkah selanjutnya ialah mencari nilai panjang garis DP memakai cara di bawah ini:

Setelah menghitung nilai DP, kemudian lihat gambar pada segitiga BDP ibarat di bawah ini:

Gambar Segitiga BDP

Dari gambar di atas sanggup diketahui bahwa BD merupakan diagonal sisi kubus sehingga panjangnya 6√2 cm. Setelah itu, kita buat permisalan nilai BO = x cm, DO = (6√2 - x) cm, dan PO = y cm. Maka dalam segitiga DOP berlaku persamaan ibarat di bawah ini:

Setelah itu dalam segitiga BOP juga berlaku persamaan ibarat di bawah ini:

Setelah diperoleh persamaan 1 dan 2, kemudian persamaan 2 disubstitusikan ke persamaan 1. Maka kesannya akan menjadi ibarat di bawah ini:

Kaprikornus jarak titik P menuju garis BD ialah 4,5√2 cm.

Sekian beberapa teladan soal dimensi tiga dan pembahasannya yang sanggup saya bagikan. Dimensi tiga ialah ilmu Matematika yang mempelajari wacana bidang, titik dan garis pada berdiri ruang serta bekerjasama pula dengan sudut dan jarak. Semoga artikel ini sanggup bermanfaat dan terima kasih telah berkunjung di blog ini.