Pengertian Himpunan Semesta dan Himpunan Bagian Beserta Contoh
Pembahasan kali ini berisi perihal pengertian himpunan semesta, pola himpunan semesta, pengertian himpunan bab dan pola himpunan bagian. Namun sebelumnya saya akan menjelaskan secara singkat mengenai himpunan bilangan. Himpunan bilangan tersebut mempunyai beberapa bab didalamnya seperti:
- Himpunan Bilangan Asli (A). Contoh A = {1, 2, 3, 4, 5, ...}
- Himpunan Bilangan Bulat (B). Contoh B = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}
- Himpunan Bilangan Cacah (C). Contoh C = {0, 1, 2, 3, 4, 5, ...}
- Himpunan Bilangan Rasional (Q). Contoh Q = {x / x = a/b , a dan b ∈ B , b ≠ 0}. Bilangan rasional sanggup dibagi menjadi dua yakni bilangan pecahan dan bilangan bulat.
- Himpunan Bilangan Prima (P) ialah bilangan yang hanya sanggup dibagi oleh 1 dan bilangan itu sendiri. Contoh P = {2, 3, 5, 7, 11, 13, ...}
Sebelum membahas perihal pengertian himpunan semesta, pola himpunan semesta, pengertian himpunan bab dan pola himpunan bagian. Saya juga akan menjelaskan perihal beberapa cara menyatakan himpunan. Berikut beberapa caranya yaitu:
Baca juga : Cara Praktis Menghitung Persen Tanpa Kalkulator Beserta Contoh
Menggunakan Kata Kata
Cara menyatakan himpunan yang pertama sanggup memakai kata kata. Misalnya:
- Himpunan aksara vokal.
- Himpunan bilangan lingkaran kurang dari 10.
Dengan Menulis Anggotanya
Cara menyatakan himpunan selanjutnya ialah dengan menulis anggotanya. Misalnya:
- B = {1, 2, 3, 4, 5}
- P = {7, 11, 13, 17, 19}
Menggunakan Notasi Pembentuk Himpunan
Cara menyatakan himpunan selanjutnya sanggup memakai notasi pembentuk himpunan. Misalnya
- C = {x / x < 10 , x bilangan cacah} dimana C merupakan semua himpunan x kurang dari 10 dan x yaitu bilangan cacah.
Himpunan Semesta
Pengertian himpunan semesta ialah himpunan yang didalamnya terdapat anggota yang sedang diperbincangkan. Himpunan ini disimbolkan dengan aksara "S".
Contoh Himpunan Semesta:
A = {2, 4, 6, 8, 10, 12}
B = {10, 11, 12, 13}
S = {2, 4, 6, 8, 10, 11, 12, 13}
Selain pengertian himpunan semesta dan pola himpunan semesta di atas. Adapula beberapa bab terkait himpunan semesta. Berikut klarifikasi selengkapnya:
Irisan Himpunan (∩)
Selain pengertian himpunan semesta dan pola himpunan semesta. Adapula pengertian irisan himpunan yaitu bab serpihan himpunan yang menjadi anggota keduanya. Misalnya saja A∩B maka himpunan anggotanya termasuk dalam anggota A dan B. Irisan himpunan disimbolkan dengan tanda "∩".
Contoh Irisan Himpunan:
A = {2, 3, 5, 7}
B = {3, 4, 5, 6, 7, 8}
A∩B = {3, 5, 7}
Gabungan (∪)
Selain pengertian himpunan semesta dan pola himpunan semesta. Adapula pengertian adonan himpunan yaitu himpunan gres yang berasal dari adonan dua himpunan dimana anggota anggotanya merupakang anggota kedua himpunan awal. Misalnya A∪B maka anggotanya merupakan kombinasi anggota A dan B. Gabungan dilambangkan dengan "∪".
Baca juga : Cara Menghitung Diagonal Sisi dan Diagonal Ruang Kubus
Contoh Gabungan Himpunan :
A = {2, 3, 5, 7}
B = {3, 4, 5, 6, 7, 8}
A∪B = {2, 3, 4, 5, 6, 7, 8}
Diagram Venn
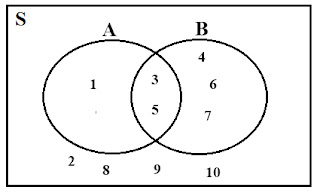
Selain pengertian himpunan semesta dan pola himpunan semesta. Adapula pengertian diagram venn ialah diagram yang menggambarkan kemungkinan menyeluruh hubungan hipotesis dan logika pada sekelompok objek. Diagram ini pertama kali ditemukan oleh ilmuan Jhon Venn dari Inggris. Diagram venn tersebut menyatakan himpunan semesta dalam bentuk persegi panjang. Sedangkan himpunan yang berada diluar himpunan semesta berbentuk noktah dan kurva sederhana. Berikut contohnya:
1. S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 3, 5}
B = {3, 4, 5, 6, 7}
A∩B = {3, 5}
A∪B = {1, 3, 4, 5, 6, 7}
Jika digambarkan dengan diagram venn akan menjadi menyerupai dibawah ini:
2. S = {0, 1, 2, 3, 4, 5, 6, 7}
A = {2, 4, 6}
B = {1, 3, 5}
Jika digambarkan dengan diagram venn akan menjadi menyerupai dibawah ini:
Himpunan Kosong ( { })
Selain pengertian himpunan semesta dan pola himpunan semesta. Adapula pengertian himpunan kosong yaitu himpunan yang tidak mempunyai anggota. Himpunan kosong dilambangkan dengan "{ }" atau "φ".
Himpunan Bagian
Pengertian himpunan bab ialah setiap himpunan yang mempunyai bagian. Himpunan ini disimbolkan dengan aksara "⊂". Misal A⊂B maka semua anggota A menjadi anggota dari B.
Contoh Himpunan Bagian:
1. A = {2, 5, 7}
B = {0, 1, 2, 3, 4, 5, 6, 7, 8}
Semua anggota A menjadi anggota B, maka A⊂B.
2. X = {a, i, u, e, o}
Y = {b, c, d}
Anggota X tidak termasuk dalam anggota Y, maka X bukan himpunan bab Y.
3. Q = {1, 2, 3}, tulislah semua himpunan bab dari Q?
Jawab.
{ }
{ 1 }
{ 2 }
{ 3 }
{ 1, 2 }
{ 1, 3 }
{ 2, 3 }
{ 1, 2, 3 }
{ 1 }
{ 2 }
{ 3 }
{ 1, 2 }
{ 1, 3 }
{ 2, 3 }
{ 1, 2, 3 }
Selain pengertian himpunan bab dan pola himpunan bab diatas. Adapula rumus untuk mencari banyaknya himpunan bab A. Berikut rumusnya:
Keterangan :
n(A) = Banyaknya anggota A
Baca juga : Rumus Persamaan Garis Lurus Beserta Contoh Soal
Cara mencari himpunan bab tersebut sanggup memakai konsep segitiga pascal. Perhatikan gambar segitiga pascal di bawah ini!
Dibawah ini terdapat pola himpunan bab lainnya. Contoh dibawah ini memakai rumus himpunan bagian.
A = {1, 3, 5, 7, 11, 13}, n (P) = 5. Berapakah banyaknya himpunan bab A?
Jawab.
Selain pengertian himpunan bab dan pola himpunan bab di atas. Adapula beberapa bab terkait himpunan bagian. Berikut klarifikasi selengkapnya:
Komplemen Himpunan
Selain pengertian himpunan bab dan pola himpunan bagian, adapula suplemen bagian. Jika dimisalkan terdapat dua himpunan A dan S. Maka suplemen himpunan A merupakan semua bab dari anggota himpunan S dan bukan dari anggota A. Komplemen himpunan ini disimbolkan dengan Aᶜ atau Aᶦ. Contohnya:
S = {1, 2, 3, 4, 5, 6}
A = (2, 3, 4, 5)
Maka Aᶜ = {1, 6} dan (Aᶜ)ᶜ = {2, 3, 4, 5}
