Usaha dan Proses dalam Termodinamika, Hukum Termodinamika 1 2 dan 3, Rumus, Contoh Soal, Kunci Jawaban - Kehadiran mesin sebagai alat pengubah energi kalor menjadi energi mekanik atau perjuangan telah mengubah kehidupan insan menjadi lebih mudah, lebih cepat, dan lebih efisien. Mesin pabrik, mesin kapal, mesin kereta api, mesin kendaraan beroda empat serta mesin motor telah meringankan perjuangan yang dibutuhkan insan untuk beraktivitas dan membuat suatu produk. Tahukah Anda peralatan lain yang memakai mesin pengubah energi kalor menjadi perjuangan dalam prinsip kerjanya? Mesin-mesin kalor tersebut ada yang memakai materi bakar solar dan dikenal sebagai mesin diesel serta ada pula yang memakai materi bakar bensin. Khusus untuk mesin berbahan bakar bensin, dikenal mesin dua tak dan mesin empat tak. Bagaimanakah cara mesin kalor bekerja? Tahukah Anda jenis perjuangan yang dilakukan mesin kalor dalam proses kerjanya? Prinsip yang mendasari cara kerja mesin kalor secara umum sanggup Anda pelajari dalam pembahasan Bab 9 ihwal termodinamika ini.
 |
| Mesin. [1] |
Pada potongan ini, Anda akan diajak untuk sanggup menerapkan konsep termodinamika dalam mesin kalor dengan cara menganalisis perubahan keadaan gas ideal dengan menerapkan aturan termodinamika.
A. Usaha dan Proses dalam Termodinamika
Termodinamika ialah cabang ilmu Fisika yang membahas ihwal kekerabatan antara panas (kalor) dan perjuangan yang dilakukan oleh kalor tersebut. Dalam melaksanakan pengamatan mengenai aliran energi antara panas dan perjuangan ini dikenal dua istilah, yaitu sistem dan lingkungan. Apakah yang dimaksud sistem dan lingkungan dalam termodinamika? Untuk memahami penggunaan kedua istilah tersebut dalam termodinamika, perhatikanlah Gambar 1. berikut.
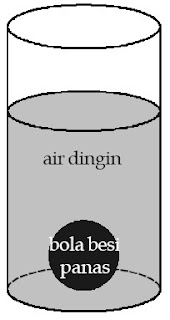 |
| Gambar 1. Bola besi dan air merupakan sistem yang diamati. Adapun, udara luar merupakan lingkungannya. |
Misalkan, Anda mengamati aliran kalor antara bola besi panas dan air dingin. Ketika bola besi tersebut dimasukkan ke dalam air. Bola besi dan air disebut sistem lantaran kedua benda tersebut menjadi objek pengamatan dan perhatian Anda. Adapun, wadah air dan udara luar disebut lingkungan lantaran berada di luar sistem, tetapi sanggup memengaruhi sistem tersebut. Dalam pembahasan termodinamika, besaran yang digunakan ialah besaran makroskopis suatu sistem, yaitu tekanan, suhu, volume, entropi, kalor, usaha, dan energi dalam.
Usaha yang dilakukan oleh sistem (gas) terhadap lingkungannya bergantung pada proses -proses dalam termodinamika, di antaranya proses isobarik, isokhorik, isotermal, dan adiabatik.
1. Usaha Sistem terhadap Lingkungannya
Pada pembahasan Bab sebelumnya, Anda telah mempelajari definisi perjuangan (W) yang dilakukan pada benda tegar, yaitu
W = F x s
Bagaimanakah cara menghitung perjuangan pada gas? Tinjaulah suatu gas yang berada dalam tabung dengan epilog berbentuk piston yang sanggup bergerak bebas, menyerupai terlihat pada Gambar 2.
 |
| Gambar 2. Ketika gas ideal di dalam tabung dipanaskan,gas tersebut memuai sehingga piston berpindah sejauh Δs. |
Ketika gas tersebut dipanaskan, piston akan berpindah sejauh Δs lantaran gas di dalam tabung memuai dari volume awal V1 menjadi volume akhir V2. Gaya yang bekerja pada piston ialah F = pA. Jika luas penampang piston (A) dan tekanan gas dalam tabung (P) berada dalam keadaan konstan, perjuangan yang dilakukan oleh gas dinyatakan dengan persamaan
W = pA Δs
Oleh lantaran A Δs = ΔV, persamaan perjuangan yang dilakukan gas sanggup ditulis menjadi :
W = p ΔV (1–1)
atau
W = p(V2 – V1) (1–2)
dengan:
p = tekanan gas (N/m2),
ΔV = perubahan volume (m3), dan
W = perjuangan yang dilakukan gas (joule).
Nilai W sanggup berharga positif atau negatif bergantung pada ketentuan berikut.
a. Jika gas memuai sehingga perubahan volumenya berharga positif, gas (sistem) tersebut dikatakan melaksanakan perjuangan yang mengakibatkan volumenya bertambah. Dengan demikian, perjuangan W sistem berharga positif.
b. Jika gas dimampatkan atau ditekan sehingga perubahan volumenya berharga negatif, pada gas (sistem) diberikan perjuangan yang mengakibatkan volume sistem berkurang. Dengan demikian, perjuangan W pada tersebut sistem ini bernilai negatif.
Usaha yang dilakukan oleh sistem sanggup ditentukan melalui metode grafik. Pada Gambar 3a sanggup dilihat bahwa proses bergerak ke arah kanan (gas memuai). Hal ini berarti V2 > V1 atau ΔV > 0 sehingga W bernilai positif (gas melaksanakan perjuangan terhadap lingkungan). W sama dengan luas tempat di bawah kurva yang diarsir (luas tempat di bawah kurva p –V dengan batas volume awal dan volume akhir)
Selanjutnya perhatikan Gambar 3b. Jika proses bergerak ke arah kiri (gas memampat), V2 < V1 atau ΔV < 0 sehingga W bernilai negatif (lingkungan melaksanakan perjuangan terhadap gas). W = – luas tempat di bawah kurva p–V yang diarsir.
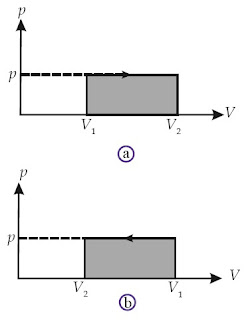 |
| Gambar 3. (a) Grafik P–V suatu gas yang mengalami pemuaian (melakukan ekspansi) (b) Grafik P–V suatu gas yang mengalami pemampatan (diberi kompresi) |
Cobalah Anda tinjau kembali Persamaan (1–1). Dari persamaan tersebut dan grafik kekerabatan tekanan (p) terhadap (V) pada Gambar 3, Anda sanggup menyimpulkan bahwa suatu sistem dikatakan melaksanakan perjuangan (W berharga positif) atau sistem diberi perjuangan (W berharga negatif), jikalau pada sistem tersebut terjadi perubahan volume ( ΔV).
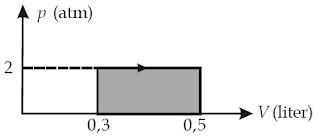
Contoh Soal 1 :
Tentukanlah perjuangan yang dilakukan gas. (1 atm = 105 N/m2)
Kunci Jawaban :
Diketahui: p = 2 atm, V1 = 0,3 L, dan V2 = 0,5 L.
1 liter = 1 dm3 = 10–3 m3
W = p ( ΔV) = p (V2 – V1)
W = 2 × 105 N/m2 (0,5 L – 0,2 L) × 10–3 m3 = 60 Joule. Contoh Soal 2 :
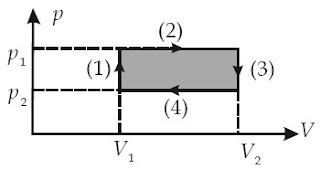
Gambar berikut memperlihatkan suatu siklus termodinamika dari suatu gas ideal.
Tentukanlah perjuangan yang dilakukan gas:
Tentukanlah perjuangan yang dilakukan gas:
a. dari keadaan A ke B,
b. dari B ke C,
c. dari C ke D,
d. dari D ke A, dan
e. dari A kembali ke A melalui B, C, dan D
Kunci Jawaban :
Diketahui: p = pB = 2 N/m2, pD = pC = 1 N/m2, VA = VD = 2 m3, dan VB = VC = 3 m3.
a. WAB = p (VB – VA) = (2 × 105 N/m2) (3 – 2) × 10–3 m3 = 200 joule
b. WBC = p (VC – VB) = 0
c. WCD= p (VD – VC) = (1 × 105 N/m2) (2 – 3) × 10–3 m3 = -100 joule
d. WDA= p (VA – VD) = 0
e. WABCDA = Wsiklus = 200 Joule + 0 – 100 Joule + 0 = 100 joule selain itu, sanggup ditentukan dengan cara :
WABCDA = Wsiklus = luas arsiran
WABCDA = (2 – 1) × 105 N/m2(3 – 2) × 10–3 m3
WABCDA = 100 joule.2. Proses dalam Termodinamika
Terdapat empat proses dalam gas pada bahasan termodinamika. Pada pembahasan Bab 8, Anda telah mengenal tiga proses, yaitu isotermal, isobarik, dan isokhorik. Proses yang keempat ialah proses adiabatik. Usaha yang terdapat pada gas yang mengalami proses-proses termodinamika tersebut akan diuraikan sebagai berikut.
a. Proses Isotermal
Proses isotermal ialah suatu proses perubahan keadaan gas pada suhu tetap.
Menurut Hukum Boyle, proses isotermal sanggup dinyatakan dengan persamaan :
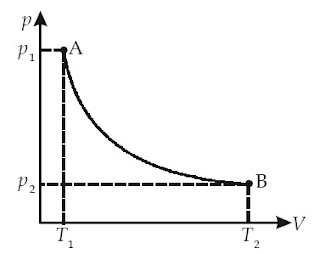 |
| Gambar 4. A–B merupakan proses isotermal. |
pV = konstan
atau
p1V1 = p2V2
Dalam proses ini, tekanan dan volume sistem berubah sehingga persamaan W = p ΔV tidak sanggup pribadi digunakan. Untuk menghitung perjuangan sistem dalam proses isotermal ini digunakan cara integral. Misalkan, pada sistem terjadi perubahan yang sangat kecil sehingga persamaan usahanya sanggup dituliskan sebagai
dW = pdV (1–3)
Jika Persamaan (1–3) diintegralkan maka sanggup dituliskan :
ò dW = ò pdV
Dari persamaan keadaan gas ideal diketahui bahwa p = nRT/V. Oleh lantaran itu, integral dari Persamaan (9–3) sanggup dituliskan menjadi :
ò dW = ò (nRT / V)
Jika konstanta n R, dan besaran suhu (T) yang nilainya tetap dikeluarkan dari integral, akan diperoleh :
W = nR T (lnV2 – lnV1)
W = n RT ln (V2/V1)
atau
Contoh Soal 3 :
Sepuluh mol gas helium memuai secara isotermal pada suhu 47 °C sehingga volumenya menjadi dua kali volume mula-mula. Tentukanlah perjuangan yang dilakukan oleh gas helium.
Kunci Jawaban :
Diketahui: T = 47 °C = (47 + 273) K = 320 K dan V2 = 2V1.
Usaha yang dilakukan gas pada proses isotermal:
W = n RT ln (V2/V1) = (10 mol) ( 8,31 J/mol)(320 K) ln (2V2/V1) = 26.592 ln 2 = 18.428 joule
b. Proses Isokhorik
Proses isokhorik ialah suatu proses perubahan keadaan gas pada volume tetap.
Menurut Hukum Gay-Lussac proses isokhorik pada gas sanggup dinyatakan dengan persamaan :
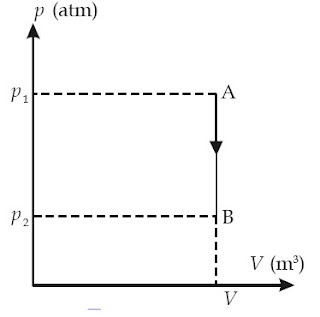 |
| Gambar 5. A–B merupakan proses isokhorik. |
p/T = konstan
atau
p1/T1 = p2/T2
Oleh lantaran perubahan volume dalam proses isokhorik ΔV = 0 maka usahanya W = 0.
c. Proses Isobarik
Proses isobarik ialah suatu proses perubahan keadaan gas pada tekanan tetap.
Menurut Hukum Charles, persamaan keadaan gas pada proses isobarik dinyatakan dengan persamaan :
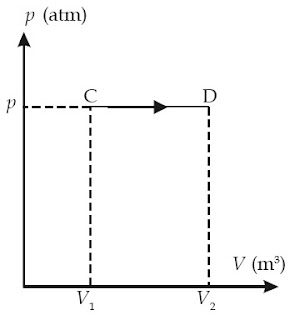 |
| Gambar 6. C–D ialah proses isobarik. |
V/T = konstan
atau
V1/T1 = V2/T2
Oleh lantaran volume sistem berubah, sedangkan tekanannya tetap, perjuangan yang dilakukan oleh sistem dinyatakan dengan persamaan
W = pΔV = p (V2 – V1) (1–5)
Contoh Soal 4 :
Suatu gas yang volumenya 1,2 liter perlahan-lahan dipanaskan pada tekanan tetap 1,5 × 105 N/m2 hingga volumenya menjadi 2 liter. Berapakah perjuangan yang dilakukan gas?
Kunci Jawaban :
Kunci Jawaban :
Diketahui: V1 = 1,2 L, V2 = 2 L, dan p = 1,5 × 105 N/m2.
Usaha yang dilakukan gas pada tekanan tetap (isobarik) adalah
W = p (V2 – V1) = (1,5 × 105 N/m2) (2 – 1,2) × 10–3 m3 = 120 joule
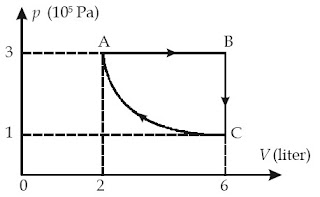
Contoh Soal 5 :
Tentukanlah:
a. perjuangan gas dari A ke B,
b. perjuangan gas dari B ke C,
c. perjuangan gas dari C ke A, dan
d. perjuangan netto gas dalam satu siklus.
Kunci Jawaban :
Diketahui: pA = pB = 3 × 105 Pa, pC = 1 × 105 Pa, VA = 2 L, dan VB = VC = 6 L.
a. Proses A ke B ialah proses isobarik. Usaha dari A ke B sanggup dihitung dengan
persamaan
WAB = p(VB – VA)
WAB = 3 × 105 Pa (6 – 2) × 10–3 m3 = 1.200 jouleb. Proses B ke C ialah proses isokhorik. Oleh lantaran VC = VB, perjuangan yang dilakukan gas WBC = 0
c. Proses dari C ke A ialah isotermal. Oleh karena pC:VC = pA:VA, perjuangan dari C ke A ialah :
WCA = nRT ln (VA/VC) = pCVC ln (VA/VC) = pAVA ln (VA/VC) (ingat: pV = nRT)
d. Usaha netto gas dalam satu siklus ABCA :
Wsiklus = WAB + WBC + WCA = 1.200 joule + 0 + (–415,8 joule) = 784,2 joule
d. Proses Adiabatik
Proses adiabatik ialah suatu proses perubahan keadaan gas di mana tidak ada kalor (Q) yang masuk atau keluar dari sistem (gas). Proses ini sanggup dilakukan dengan cara mengisolasi sistem memakai materi yang tidak gampang menghantarkan kalor atau disebut juga materi adiabatik. Adapun, bahan-bahan yang bersifat gampang menghantarkan kalor disebut materi diatermik
Proses adiabatik ini mengikuti persamaan Poisson sebagai berikut
p Vγ = konstan
atau
p1 V1γ = p2 V2γ (1–6)
Oleh lantaran persamaan gas ideal dinyatakan sebagai pV = nRT maka Persamaan (9–4) sanggup ditulis :
T1V1(γ –1) = T2 V2(γ –1) (1–7)
dengan γ = CP/CV = konstanta Laplace, dan CP/CV > 1. CP ialah kapasitas kalor gas pada tekanan tetap dan CV adalah kalor gas pada volume tetap. Perhatikan diagram p – V pada Gambar 7.
Dari kurva kekerabatan p – V tersebut, Anda sanggup mengetahui bahwa:
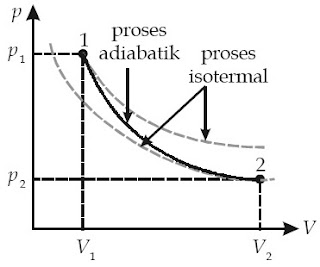 |
| Gambar 7. Pada proses adiabatik, kurva p–V lebih curam dibandingkan dengan kurva p–V pada proses isotermal. |
1) Kurva proses adiabatik lebih curam daripada kurva proses isotermal.
2) Suhu, tekanan, maupun volume pada proses adiabatik tidak tetap.
Oleh lantaran sistem tidak melepaskan atau mendapatkan kalor, pada kalor sistem proses adiabatik Q sama dengan nol. Dengan demikian, perjuangan yang dilakukan oleh sistem hanya mengubah energi dalam sistem tersebut. Besarnya perjuangan pada proses adiabatik tersebut dinyatakan dengan persamaan berikut.
W= 3/2 nRT−T = 3/2 (p1 V1 − p2 V2) (1–8)
Catatan Fisika :
OTEC (Ocean Thermal Energy Conversion) ialah sebuah pembangkit tenaga listrik mini. Mesin ini bekerja berdasarkan perbedaan suhu antara permukaan maritim yang hangat dan kedalaman maritim yang dingin. Pusat pembangkit listrik ini bebas polusi.
Contoh Soal 6 :
OTEC
 |
| OTEC di Hawai. [2] |
Contoh Soal 6 :
Sebuah mesin mempunyai rasio pemampatan 12 : 1 yang berarti bahwa sesudah pemampatan, volume gas menjadi 1/12 volume awalnya. Anggap materi bakar bercampur udara pada suhu 35 °C, tekanan 1 atm, dan γ = 1,4. Jika proses pemampatan terjadi secara adiabatik, hitunglah tekanan pada keadaan tamat dan suhu campuran.
Kunci Jawaban :
Diketahui: V2 = 1/12 V1, T1 = 35 + 273 = 308 K, dan p1 = 1 atm.
Untuk memilih tekanan akhir p2, gunakan rumus :
p2 = 32,4 atm.
Suhu adonan atau suhu akhir T2 diperoleh sebagai berikut :
Suhu adonan atau suhu akhir T2 diperoleh sebagai berikut :
T2 = 308 K (12)1,4 – 1 = 308 K (12)0,4 = 832 K = 559 °C
Contoh Soal 7 :
Usaha sebesar 2 × 103 J diberikan secara adiabatik untuk memampatkan 0,5 mol gas ideal monoatomik sehingga suhu mutlaknya menjadi 2 kali semula. Jika konstanta umum gas R = 8,31 J/mol K, tentukanlah suhu awal gas.
Kunci Jawaban :
Diketahui: W = 2 × 103 J, T2 = 2T1, dan n = 0,5 mol.
T1 = 2W / 3nR = 2(2 x 103 joule) / 3 x 0,5 mol x 8,31 J/molK = 321 K
W = 3/2 n R (T2 – T1) = 3/2 n R (2T1 – T1)
W = 3/2 n R T1
Jadi, suhu awal gas ialah 321 K.
Dari pembahasan materi Bab 8, Anda telah mengetahui bahwa suhu gas berafiliasi dengan energi kinetik yang dimiliki oleh gas tersebut. Anda juga telah mempelajari kekerabatan antara energi kinetik dan energi dalam yang dimiliki oleh gas. Perubahan energi dalam sanggup terjadi jikalau terjadi perubahan suhu (energi dalam akan meningkat jikalau suhu gas (sistem) meningkat atau pada gas diberikan kalor). Apakah perubahan energi dalam sanggup terjadi pada gas yang diberi atau melaksanakan perjuangan mekanik?
Hubungan antara kalor yang diterima atau dilepaskan suatu sistem, perjuangan yang dilakukan pada sistem, serta perubahan energi dalam sistem yang ditimbulkan oleh kalor dan perjuangan tersebut dijelaskan dalam Hukum Pertama Termodinamika.
Hukum Pertama Termodinamika ialah perluasan bentuk dari Hukum Kekekalan Energi dalam mekanika. Hukum ini menyatakan bahwa: "Jumlah kalor pada suatu sistem sama dengan perubahan energi dalam sistem tersebut ditambah perjuangan yang dilakukan oleh sistem."
Dengan demikian, meskipun energi kalor sistem telah berkembang menjadi energi mekanik (usaha) dan energi dalam, jumlah seluruh energi tersebut selalu tetap. Secara matematis, Hukum Pertama Termodinamika dituliskan sebagai berikut.
Q = ΔU + W (1–9)
dengan:
Q = kalor yang diterima atau dilepaskan oleh sistem,
ΔU = U2 — U1 = perubahan energi dalam sistem, dan
W = perjuangan yang dilakukan sistem.
Perjanjian tanda yang berlaku untuk Persamaan (1-9) tersebut ialah sebagai berikut.
1. Jika sistem melaksanakan kerja maka nilai W berharga positif.
2. Jika sistem mendapatkan kerja maka nilai W berharga negatif
3. Jika sistem melepas kalor maka nilai Q berharga negatif
4. Jika sistem mendapatkan kalor maka nilai Q berharga positif
Contoh Soal 8 :
Delapan mol gas ideal dipanaskan pada tekanan tetap sebesar 2 × 105 N/m2 sehingga volumenya berubah dari 0,08 m3 menjadi 0,1 m3. Jika gas mengalami perubahan energi dalam gas sebesar 1.500 J, berapakah kalor yang diterima gas tersebut.
Kunci Jawaban :
Diketahui: p = 2 × 105 N/m2, V1 = 0,08 m3, V2 = 0,1 m3, dan ΔU = 1.500 J.
Q = ΔU+ W
Q = ΔU + p(V2 – V1)
Q = 1.500 joule + 2 × 105 N/m2 (0,1 – 0,08) m3 = 1.500 joule + 4.000 joule = 5.500 J Contoh Soal 9 :
Suatu sistem mengalami proses isobarik. Pada sistem dilakukan perjuangan sebesar 100 J. Jika perubahan energi dalam sistem ΔU dan kalor yang diserap sistem = 150 joule, berapakah besarnya ΔU?
Kunci Jawaban :
Diketahui: W = –100 joule (dilakukan usaha), dan Q = 150 joule (sistem menyerap kalor).
Menurut Hukum Pertama Termodinamika
ΔU = Q – W = 150 joule – (–100 joule) = 250 joule.
Catatan Fisika :
Hero atau Heron membuat mesin uap pertama yang disebut aeolipile. Mesin ini terdiri atas sebuah pemanas yang terletak di bawah suatu kuali dan mempunyai dua lubang angin. Uap yang dialirkan ke dalam kuali akan keluar dari lubang angin sehingga akan memutar kincir. Aeolipile tidak mempunyai fungsi praktis. (Sumber: Jendela Iptek, 1997)
1. Perubahan Energi Dalam
Perubahan energi dalam ΔU tidak bergantung pada proses bagaimana keadaan sistem berubah, tetapi hanya bergantung pada keadaan awal dan keadaan tamat sistem tersebut.
Anda telah mengetahui bahwa proses-proses dalam termodinamika terbagi atas empat jenis, yaitu isotermal, isokhorik, isobarik, dan adiabatik. Perubahan energi dalam terjadi pada setiap proses tersebut dijelaskan sebagai berikut.
a. Proses Isotermal
Anda telah memahami bahwa proses isotermal merupakan suatu proses yang terjadi dalam sistem pada suhu tetap. Besar perjuangan yang dilakukan sistem proses isotermal ini ialah W = nRT In (V2/V1). Oleh lantaran ΔT = 0, berdasarkan Teori Kinetik Gas, energi dalam sistem juga tidak berubah (ΔU = 0) lantaran perubahan energi dalam bergantung pada perubahan suhu. Ingatlah kembali persamaan energi dalam gas monoatomik yang dinyatakan dalam persamaan ΔU = 3/2 nRΔTyang telah dibahas pada Bab 8.
Dengan demikian, persamaan Hukum Pertama Termodinamika untuk proses isotermal ini sanggup dituliskan sebagai berikut.
Q = ΔU + W = 0 + W
Q = W = nR T ln (V2/V1) (1 -10)
b. Proses Isokhorik
Dalam proses isokhorik perubahan yang dialami oleh sistem berada dalam keadaan volume tetap. Anda telah memahami bahwa besar perjuangan pada proses isokhorik dituliskan W = pΔV = 0. Dengan demikian, persamaan Hukum Pertama Termodinamika untuk proses ini dituliskan sebagai
Q = ΔU + W = ΔU + 0
Q = ΔU = U2 - U1 (1-11)
Dari Persamaan (1-11) Anda sanggup menyatakan bahwa kalor yang diberikan pada sistem hanya digunakan untuk mengubah energi dalam sistem tersebut. Jika persamaan energi dalam untuk gas ideal monoatomik disubstitusikan ke dalam Persamaan (1-11), didapatkan perumusan Hukum
Pertama Termodinamika pada proses isokhorik sebagai berikut.
Q = ΔU = 3/2 nR ΔT (1-12)
atau
Q = U2 - U1 = 3/2 nR (T2 —T1) (1-13)
c. Proses Isobarik
Jika gas mengalami proses isobarik, perubahan yang terjadi pada gas berada dalam keadaan tekanan tetap. Usaha yang dilakukan gas dalam proses ini memenuhi persamaan W = P ΔV = p(V2 – V1). Dengan demikian, persamaan Hukum Pertama Termodinamika untuk proses isobarik sanggup dituliskan sebagai berikut.
Q = ΔU + W
Q = ΔU + p(V2 – V1) (9-14)
Untuk gas ideal monoatomik, Persamaan (1-14) sanggup dituliskan sebagai :
Q = 3/2 nR (T2 —T1) + p (V2 – V1) (1-15)
d. Proses adiabatik
Dalam pembahasan mengenai proses adiabatik, Anda telah mengetahui bahwa dalam proses ini tidak ada kalor yang keluar atau masuk ke dalam sistem sehingga Q = 0. Persamaan Hukum Pertama Termodinamika untuk proses adiabatik ini sanggup dituliskan menjadi
Q = ΔU + W
0 = ΔU + W
atau
W = - ΔU = - (U2 - U1) (1-16)
Berdasarkan Persamaan (1-16) tersebut, Anda sanggup menyimpulkan bahwa perjuangan yang dilakukan oleh sistem akan mengakibatkan terjadinya perubahan energi dalam sistem di mana energi dalam tersebut sanggup bertambah atau berkurang dari keadaan awalnya.
Persamaan Hukum Pertama Termodinamika untuk gas ideal monoatomik pada proses adiabatik ini dituliskan sebagai :
W = - ΔU = - 3/2 nR (T2 —T1) (1-17)
Catatan Fisika :
Energi dalam secangkir kopi hanya bergantung pada keadaan termodinamikanya (seberapa banyak kopi dan air yang dikandungnya, dan berapa suhunya). Energi tersebut tidak bergantung pada proses persiapan kopinya, yaitu lintasan termodinamika yang membawanya ke keadaan yang sekarang. (Sumber: Fisika Universitas, 2000)
2. Kapasitas Kalor
Kapasitas kalor gas ialah banyaknya kalor yang dibutuhkan untuk menaikkan suhu gas sebesar 1°C, untuk volume tetap disebut CV dan untuk tekanan tetap disebut Cp.
Secara matematis, kapasitas kalor (C) dinyatakan dengan persamaan :
C = Q/ΔT (1–18)
Pada gas, perubahan suhu sanggup dilakukan dengan proses isobarik atau proses isokhorik. Dengan demikian, kapasitas kalor gas sanggup dibedakan menjadi dua, yakni kapasitas kalor pada tekanan tetap (Cp) dan kapasitas kalor pada volume tetap (V). Perumusan kedua pada kapasitas kalor tersebut secara matematis sanggup dituliskan sebagai berikut.
Cp = QP/ΔT dan CV = QV/ΔT (1–19)
Jika besaran QP dan QV dimasukkan ke dalam persamaan Hukum Pertama Termodinamika, akan didapatkan persamaan berikut.
a. Pada proses isokhorik
QV = ΔU + W (1–20)
Oleh lantaran dalam proses ini volume sistem tetap (ΔU = 0) maka perjuangan sistem W = 0 sehingga didapatkan persamaan :
QV = ΔU (1–21)
b. Pada proses isobarik
QP = ΔU + W
Oleh lantaran dalam proses ini tekanan sistem tetap ( Δp + 0), perjuangan sistem W = p ΔV. Dengan demikian, persamaan Hukum Pertama Termodinamika sanggup dituliskan
QP = ΔU + p ΔV (1–22)
Dengan melaksanakan substitusi Persamaan (1–21) ke Persamaan (1–22) sanggup dituliskan persamaan
Qp = ΔU + p ΔV atau Qp – QV = p ΔV (1–23)
Selanjutnya, jikalau Persamaan (9–19) disubstitusikan Persamaan (1–23) akan diperoleh persamaan
(Cp ΔT) – (CV ΔT) = p ΔV
(Cp CV)ΔT = p ΔV
Berdasarkan persamaan keadaan gas ideal pV = nRT, Persamaan (1–24) sanggup dituliskan menjadi
Cp – CV = nR (1–25)
Untuk gas monoatomik, energi dalam gas dinyatakan dengan persamaan :
ΔU = 3/2 nRΔT
Dengan demikian, kapasitas kalor pada proses isokhorik (QV = ΔU) sanggup dituliskan sebagai :
CV = 3/2 nR (9–26)
Catatan Fisika :
Umumnya memasak melibatkan proses isobarik. Hal ini disebabkan lantaran tekanan udara di atas panci, wajan, atau dalam panggangan microwave tetap konstan sementara makanan dipanaskan. (Sumber: Fisika Universitas, 2000)
Besar Cp dapat ditentukan dari Persamaan (1–25) sehingga diperoleh :
Cp = CV + nR
Cp = 3/2 nR + nR
Contoh Soal 10 :
Gas nitrogen bermassa 56 × 10–3 kg dipanaskan dari suhu 270 K menjadi 310 K. Jika nitrogen ini dipanaskan dalam baskom yang bebas memuai, dibutuhkan kalor sebanyak 2,33 kJ. Jika gas nitrogen ini dipanaskan dalam baskom kaku (tidak sanggup memuai), dibutuhkan kalor sebesar 1,66 kJ. Jika massa molekul relatif nitrogen 28 g/mol, hitunglah kapasitas kalor gas nitrogen dan tetapan umum gas.
Kunci Jawaban :
Diketahui: m = 56 × 10–3 kg, ΔT = 40 K, dan Mr = 28 g/mol = 28 × 10–3 kg/mol.
a. Proses tekanan tetap pada gas:
Qp = 2,33 kJ = 2.330 J
Qp = Cp ( ΔT)
2.330 J = Cp (40 K) → Cp = 58, 2 J/K.Proses volume tetap pada gas:
QV = 1,66 kJ = 1.660 J.
QV = CV ( ΔT)
1.660 joule = CV (40 K) → CV = 41,5 J/Kb. Tetapan umum gas R dihitung sebagai berikut.
Cp – CV = n R = (m/Mr) R → R = Mr/m (CP – CV)
Sadi Carnot ialah seorang ilmuwan yang lahir di Paris, Prancis. Sebagian besar waktunya ia gunakan untuk memeriksa mesin uap. Pada 1824, ia mempublikasikan esai yang berjudul Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance. Penemuannya menjadi dasar ilmu termodinamika dan memperlihatkan manfaat besar terhadap kehidupan manusia. (Sumber: www.all iographies.com)
3. Siklus Carnot dan Efisiensi Mesin
Keadaan suatu sistem dalam termodinamika sanggup berubah-ubah, berdasarkan percobaan besaran-besaran keadaan sistem tersebut. Namun, besaran-besaran keadaan tersebut hanya berarti jikalau sistem berada dalam keadaan setimbang. Misalnya, jikalau Anda mengamati suatu gas yang sedang memuai di dalam tabung, temperatur dan tekanan gas tersebut di setiap potongan tabung sanggup berubah-ubah. Oleh lantaran itu, Anda tidak sanggup memilih suhu dan temperatur gas ketika kedua besaran tersebut masih berubah. Agar sanggup memilih besaran-besaran keadaan gas, gas harus dalam keadaan reversibel. Apakah yang dimaksud dengan proses reversibel?
Proses reversibel ialah suatu proses dalam sistem di mana sistem hampir selalu berada dalam keadaan setimbang.
Perhatikanlah Gambar 8.
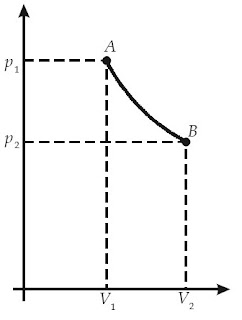 |
| Gambar 8. Perubahan keadaan gas dalam siklus reversibel. |
Dalam kenyataannya, sulit untuk menemukan proses reversibel lantaran proses ini tidak memperhitungkan energi yang hilang dari dalam sistem (misalnya, gesekan). Namun, proses reversibel memenuhi Hukum Pertama Termodinamika. Tahukah Anda yang dimaksud dengan siklus termodinamika? Siklus termodinamika ialah proses yang terjadi pada sistem sehingga kesudahannya sistem kembali pada keadaan awalnya.
Prinsip siklus termodinamika ini kali pertama dijelaskan oleh seorang insinyur Perancis berjulukan Sadi Carnot dan disebut siklus Carnot. Siklus Carnot ialah suatu siklus ideal reversibel yang terdiri atas dua proses isotermal dan proses adiabatik, menyerupai terlihat pada Gambar 9.
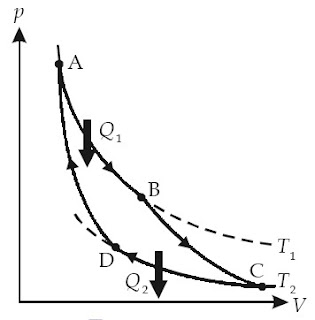 |
| Gambar 9. Siklus Carnot. |
Siklus Carnot ini merupakan salah satu prinsip dasar siklus termodinamika yang digunakan untuk memahami cara kerja mesin Carnot. Perhatikanlah Gambar 10. berikut.
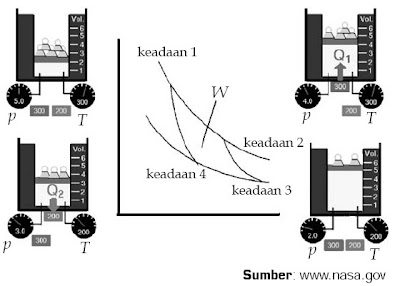 |
| Gambar 10. Siklus Carnot pada mesin Carnot. |
Pada gambar tersebut suatu gas ideal berada di dalam silinder yang terbuat dari materi yang tidak gampang menghantarkan panas. Volume silinder tersebut sanggup diubah dengan cara memindahkan posisi pistonnya. Untuk mengubah tekanan gas, diletakkan beberapa beban di atas piston. Pada sistem gas ini terdapat dua sumber kalor yang disebut reservoir suhu tinggi (memiliki suhu 300 K) gas mempunyai temperatur tinggi (300 K), tekanan tinggi (4 atm), dan volume rendah (4 m3).
Berikut urutan keempat langkah proses yang terjadi dalam siklus Carnot.
a. Pada langkah, gas mengalami perluasan isotermal. Reservoir suhu tinggi menyentuh dasar silinder dan jumlah beban di atas piston dikurangi. Selama proses ini berlangsung, temperatur sistem tidak berubah, namun volume sistem bertambah. Dari keadaan 1 ke keadaan 2, sejumlah kalor (Q1) dipindahkan dari reservoir suhu tinggi ke dalam gas.
b. Pada langkah kedua, gas berubah dari keadaan 2 ke keadaan 3 dan mengalami proses perluasan adiabatik. Selama proses ini berlangsung, tidak ada kalor yang keluar atau masuk ke dalam sistem. Tekanan gas diturunkan dengan cara mengurangi beban yang ada di atas piston. Akibatnya, temperatur sistem akan turun dan volumenya bertambah.
c. Pada langkah ketiga, keadaan gas berubah dari keadaan 3 ke keadaan 4 melalui proses kompresi isotermal. Pada langkah ini, reservoir suhu rendah (200 K) menyentuh dasar silinder dan jumlah beban di atas piston bertambah. Akibatnya tekanan sistem meningkat, temperaturnya konstan, dan volume sistem menurun. Dari keadaan 3 ke keadaan 4, sejumlah kalor (Q2) dipindahkan dari gas ke reservoir suhu rendah untuk menjaga temperatur sistem supaya tidak berubah.
d. Pada langkah keempat, gas mengalami proses kompresi adiabatik dan keadaannya berubah dari keadaan 4 ke keadaan1. Jumlah beban di atas piston bertambah. Selama proses ini berlangsung, tidak ada kalor yang keluar atau masuk ke dalam sistem, tekanan sistem meningkat, dan volumenya berkurang.
Menurut kurva kekerabatan p–V dari siklus Carnot, perjuangan yang dilakukan oleh gas ialah luas tempat di dalam kurva p–V siklus tersebut. Oleh lantaran siklus selalu kembali ke keadaannya semula, ΔUsiklus = 0 sehingga persamaan perjuangan siklus (Wsiklus) sanggup dituliskan menjadi
Wsiklus = ΔQsiklus = (Q1 – Q2) (1–28)
dengan:
Q1 = kalor yang diserap sistem, dan
Q2 = kalor yang dilepaskan sistem.
Ketika mesin mengubah energi kalor menjadi energi mekanik (usaha). Perbandingan antara besar perjuangan yang dilakukan sistem (W) terhadap energi kalor yang diserapnya (Q1) disebut sebagai efisiensi mesin. Persamaan matematis efisiensi mesin ini dituliskan dengan persamaan :
η = (W/Q1) x 100 % (1–29)
dengan η = efisiensi mesin.
Oleh lantaran perjuangan dalam suatu siklus termodinamika dinyatakan dengan
W = Q1 – Q2
maka Persamaan (1–30) sanggup dituliskan menjadi :
η = (Q1 - Q2 / Q1) x 100 %
Pada mesin Carnot, besarnya kalor yang diserap oleh sistem (Q1) sama dengan temperatur reservoir suhu tingginya (T1). Demikian juga, besarnya kalor yang dilepaskan sistem (Q2) sama dengan temperatur reservoir suhu rendah mesin Carnot tersebut. Oleh lantaran itu, Persamaan (1–30) sanggup dituliskan menjadi :
Dari Persamaan (1–31) tersebut, Anda sanggup menyimpulkan bahwa efisiensi mesin Carnot sanggup ditingkatkan dengan cara menaikkan temperatur reservoir suhu tinggi atau menurunkan temperatur reservoir suhu rendah.
Catatan Fisika :
Lokomotif uap ini bekerja dengan memakai aturan pertama termodinamika. Saat panas dihasilkan oleh batubara atau kayu yang dibakar dalam mesin lokomotif, sebagian energi menaikkan suhu air (yang mendidih dan menghasilkan uap) dalam mesin. Sisa energi digunakan guna mengekspansikan uap untuk menghasilkan kerja dan menggerakkan lokomotif. (Sumber: Fisika Universitas, 1998)
Contoh Soal 11 :
Sebuah mesin gas ideal bekerja dalam suatu siklus Carnot antara suhu tinggi T1 °C dan dan suhu rendah 127 °C. Jika mesin menyerap kalor 60 kkal pada suhu tertinggi dan membuang kalor 48 kkal, hitunglah:
a. perjuangan yang dihasilkan dalam satu siklus,
b. efisiensi mesin tersebut, dan
c. besarnya suhu tinggi T1.
Kunci Jawaban :
Diketahui: T2 = 127 °C, Q1 = 60 kkal, dan Q2 = 48 kkal.
a. Berdasarkan Hukum Pertama termodinamika:
W = Q1 – Q2 = 60 kkal – 48 kkal = 12 kkal
b. Efisiensi mesin Carnot
η = (W/Q1) x 100 % = (12 kkal / 60 kkal) x 100 % = 20%
c. Efisiensi mesin dalam bentuk suhu dinyatakan dengan persamaan :
Contoh Soal 12 :
Sebuah mesin Carnot yang memakai reservoir suhu tinggi bersuhu 800 K mempunyai efisiensi 40%. Agar efisiensi maksimumnya naik menjadi 50%, tentukanlah kenaikan suhu yang harus dilakukan pada reservoir suhu tinggi.
Kunci Jawaban :
Diketahui: T1 = 800 K, η1 = 40%, dan η2 = 50%.
Cara umum
• Efisiensi mesin semula η1 = 40%
• Agar efisiensi menjadi η2 = 50% untuk T2 = 480 K
Jadi, temperatur suhu tinggi harus dinaikkan menjadi 960 K.
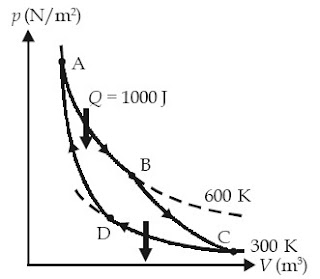
Contoh Soal 13 :
Suatu mesin Carnot bekerja di antara suhu 600 K dan 300 K serta mendapatkan kalor sebesar 1.000 joule (seperti terlihat pada gambar). Usaha yang dilakukan mesin dalam satu siklus ialah ....
a. 300 J
b. 400 J
c. 500 J
d. 600 J
e. 700 J
Kunci Jawaban :
W = 500 joule
Jawab: c
1. Entropi
Pada pembahasan mengenai siklus Carnot dan mesin Carnot, proses termodinamika yang terjadi selama proses tersebut bisa mengubah seluruh energi kalor menjadi perjuangan dan tidak ada energi yang hilang. Siklus termodinamika yang telah dibahas pada subbab B merupakan siklus ideal yang tidak pernah ditemui dalam kehidupan nyata.
Sebagai pola sederhana, missalkan Anda memasukkan sebuah bola besi panas ke dalam baskom yang berisi air dingin. Anda tentunya telah memahami bahwa kalor akan berpindah dari bola besi ke air sehingga suhu keduanya sama atau dikatakan keduanya telah berada dalam kesetimbangan termal. Namun, jikalau Anda membalik proses ini dengan cara memasukkan bola besi hambar ke dalam air panas, mungkinkah suhu bola besi tersebut naik dan suhu air turun dan keduanya mencapai kesetimbangan termal yang sama, menyerupai pada keadaan sebelumnya?
Proses termodinamika yang melaksanakan proses aliran kalor dari benda (reservoir) bersuhu rendah ke benda (reservoir) bersuhu tinggi, menyerupai yang dimisalkan tersebut mustahil terjadi secara impulsif (tanpa ada perjuangan yang diberikan ke dalam sistem).
Hal inilah yang kemudian diteliti oleh Clausius dan Kelvin-Planck sehingga menghasilkan rumusan Hukum Kedua Termodinamika. Berikut pernyataan Kevin-Planck dan Clausius.
a. Menurut Clausius, kalor tidak sanggup berpindah dari benda bersuhu rendah ke benda bersuhu tinggi tanpa adanya perjuangan luar yang diberikan kepada sistem.
b. Menurut Kelvin-Planck, mustahil membuat mesin yang bekerja dalam suatu siklus dan menghasilkan seluruh kalor yang diserapnya menjadi usaha.
Dalam menyatakan Hukum Kedua Termodinamika ini, Clausius memperkenalkan besaran gres yang disebut entropi (S). Entropi ialah besaran yang menyatakan banyaknya energi atau kalor yang tidak sanggup diubah menjadi usaha. Ketika suatu sistem menyerap sejumlah kalor Q dari reservoir yang mempunyai temperatur mutlak, entropi sistem tersebut akan meningkat dan entropi reservoirnya akan menurun sehingga perubahan entropi sistem sanggup dinyatakan dengan persamaan :
ΔS = Q/T (1–32)
Persamaan (32) tersebut berlaku pada sistem yang mengalami siklus reversibel dan besarnya perubahan entropi (ΔS) hanya bergantung pada keadaan tamat dan keadaan awal sistem.
Tokoh Fisika :
Watt ialah seorang ilmuwan dan insinyur besar yang berasal dari Britania. Ia membuat mesin uap pertama, yang menjadi kekuatan utama terjadinya Revolusi Industri Eropa.
Contoh Soal 14 :
Gambar di atas memperlihatkan bahwa 1.200 J kalor mengalir secara impulsif dari reservoir panas bersuhu 600 K ke reservoir hambar bersuhu 300 K. Tentukanlah jumlah entropi dari sistem tersebut. Anggap tidak ada perubahan lain yang terjadi.
Kunci Jawaban :
Diketahui : Q = 1.200 J, T1 = 600 K, dan T2 = 300 K.
Perubahan entropi reservoir panas:
ΔS1 = (- Q1/T1) = (-1.200 J/600 K) = –2 J/K
Perubahan entropi reservoir dingin:
ΔS2 = (Q2/T2) = (1.200 J/300 K) = –4 J/K
Total perubahan entropi total ialah jumlah aljabar perubahan entropi setiap reservoir:
ΔSsistem = ΔS1 + ΔS2 = –2 J/K + 4 J/K = +2 J/K
2. Mesin Pendingin (refrigerator)
Kalor sanggup dipaksa mengalir dari benda hambar ke benda panas dengan melaksanakan perjuangan pada sistem. Peralatan yang bekerja dengan cara menyerupai ini disebut mesin pendingin (refrigerator). Contohnya lemari es dan pendingin ruangan (Air Conditioner). Perhatikan Gambar 11.
 |
| Gambar 11. Skema kerja mesin pendingin (refrigerator). |
Ukuran kemampuan sebuah mesin pendingin dinyatakan sebagai koefisien daya guna (koefisien performansi) yang diberi lambang Kp dan dirumuskan dengan persamaan :
Kr = Q2 / W (1–33)
Oleh lantaran perjuangan yang diberikan pada mesin pendingin tersebut dinyatakan dengan W = Q1 - Q2, Persamaan (1–33) sanggup ditulis menjadi :
Kr = Q2 / (Q1 - Q2) (1–34)
Jika gas yang digunakan dalam sistem mesin pendingin ialah gas ideal, Persamaan (1–34) sanggup dituliskan menjadi :
Kp = T2 / (T1 - T1) (1–35)
Lemari es dan pendingin ruangan mempunyai koefisien performansi dalam jangkauan 2 hingga dengan 6. Semakin tinggi nilai KP, semakin baik mesin pendingin tersebut.
Contoh Soal 15 :
Sebuah lemari es mempunyai koefisien performansi 6. Jika suhu ruang di luar lemari es ialah 28 °C, berapakah suhu paling rendah di dalam lemari es yang sanggup diperoleh?
Kunci Jawaban :
Diketahui: Kp = 6, dan T1 = 28° C.
Koefisien performansi maksimum diperoleh sebagai berikut:
dengan T1 ialah suhu tinggi dan T2 ialah suhu rendah. Dari persamaan tersebut diperoleh
(KP) T1 – (KP) T2 = T2
(KP) T1 = (1 + KP) T2 Dari soal diketahui T1 = (28 + 273) K = 301 K dan KP = 6,0 sehingga suhu paling rendah di dalam lemari es T2 dapat dihitung.
T2 = 258 K atau –15 °C.
Contoh Soal 16 :
Sebuah mesin Carnot mendapatkan 2.000 J dari reservoir panas dan melepaskan 1.750 J pada reservoir dingin. Dengan demikian, efisiensi mesin tersebut ialah ....
a. 6,25%
b. 10%
c. 12,5%
d. 25%
e. 87,5%
Kunci Jawaban :
Informasi yang diketahui dari soal:
Q1 = 2.000 J
Q2 = 1.750 J
Usaha yang dilakukan oleh mesin Carnot adalah
W = Q2 – Q1
η = (W/Q1) x 100 %
η = 12,5%
Jawab: c
D. Hukum Termodinamika 3
Hukum ketiga termodinamika terkait dengan temperatur nol absolut. Hukum ini menyatakan bahwa pada ketika suatu sistem mencapai temperatur nol absolut, semua proses akan berhenti dan entropi sistem akan mendekati nilai minimum. Hukum ini juga menyatakan bahwa entropi benda berstruktur kristal tepat pada temperatur nol adikara bernilai nol. [8]
Rangkuman :
1. Sistem dalam termodinamika ialah potongan ruang atau benda yang menjadi sentra perhatian pengamatan.
2. Lingkungan dalam termodinamika ialah segala sesuatu yang berada di luar sistem dan memengaruhi sistem.
3. Hukum Pertama Termodinamika menyatakan bahwa jumlah energi yang diberikan pada sistem sama dengan perubahan energi dalam sistem ditambah perjuangan yang dilakukannya :
Q = ΔU +W
4. a. Pada proses isokhorik, ΔW = 0
b. Pada proses isotermal, ΔU = 0
c. Pada proses adiabatik, Q = 0
5. Hukum Kedua Termodinamika memberi batasan terhadap perubahan energi yang sanggup berlangsung atau tidak sanggup berlangsung.
6. Entropi ialah suatu ukuran banyaknya kalor yang tidak sanggup diubah menjadi usaha.
ΔS = Q/T
7. Mesin kalor mengubah energi termal menjadi perjuangan dengan cara memindahkan kalor dari reservoir bersuhu tinggi ke reservoir bersuhu rendah.
8. Efisiensi mesin kalor
9. Mesin pendingin memerlukan perjuangan untuk memindahkan kalor dari reservoir bersuhu rendah ke reservoir bersuhu tinggi.
10. Efisiensi mesin pendingin :
Anda kini sudah mengetahui Termodinamika dan Hukum Termodinamika. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.
Referensi :
Saripudin, A., D. Rustiawan K., dan A. Suganda. 2009. Mudah Belajar Fisika 1 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah Program Ilmu Pengetahuan Alam. Pusat Perbukuan Departemen Nasional, Departemen Pendidikan Nasional, Jakarta. p. 234.
Referensi Lainnya :
Tim Redaksi Dorling Kindersley. 1997. Jendela IPTEK, Cetakan Pertama. Jakarta: Balai Pustaka.
[1] http://en.wikipedia.org/wiki/Engine
[2] http://en.wikipedia.org/wiki/Ocean_thermal_energy_conversion
[3] http://modelengines.info/aeolipile/
[4] http://en.wikipedia.org/wiki/Coffee
[5] http://en.wikipedia.org/wiki/Nicolas_L%C3%A9onard_Sadi_Carnot
[6] http://id.wikipedia.org/wiki/Lokomotif_uap
[7] http://en.wikipedia.org/wiki/James_Watt
[8] http://id.wikipedia.org/wiki/Termodinamika
Referensi :
Saripudin, A., D. Rustiawan K., dan A. Suganda. 2009. Mudah Belajar Fisika 1 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah Program Ilmu Pengetahuan Alam. Pusat Perbukuan Departemen Nasional, Departemen Pendidikan Nasional, Jakarta. p. 234.
Referensi Lainnya :
Tim Redaksi Dorling Kindersley. 1997. Jendela IPTEK, Cetakan Pertama. Jakarta: Balai Pustaka.
[1] http://en.wikipedia.org/wiki/Engine
[2] http://en.wikipedia.org/wiki/Ocean_thermal_energy_conversion
[3] http://modelengines.info/aeolipile/
[4] http://en.wikipedia.org/wiki/Coffee
[5] http://en.wikipedia.org/wiki/Nicolas_L%C3%A9onard_Sadi_Carnot
[6] http://id.wikipedia.org/wiki/Lokomotif_uap
[7] http://en.wikipedia.org/wiki/James_Watt
[8] http://id.wikipedia.org/wiki/Termodinamika