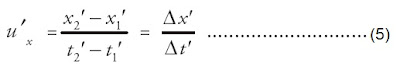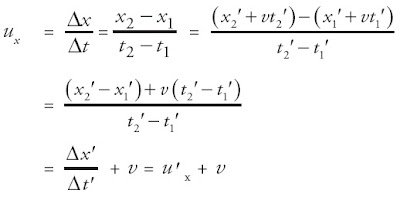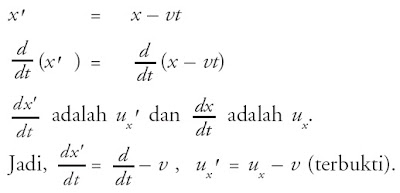LIRIK LAGU : Pintar Pelajaran Pengertian Teori Relativitas Khusus, Relativitas Newton, Transformasi Galileo, Rumus, Rujukan Soal, Jawaban, Fisika

Pengertian fisika" target="_blank">Teori Relativitas Khusus, Relativitas Newton, Transformasi Galileo, Rumus, Contoh Soal, Jawaban, Fisika - Coba kalian perhatikan gambar 1. Lekukan di bidang jala menggambarkan gravitasi sebagai hasil distorsi ruang di sekitarnya. Matahari yang terlihat pada cuilan kiri, walaupun jauh lebih berat dibandingkan bumi, hanya bisa menghasilkan lekuk kecil bila dibanding bintang neutron (tengah) yang berukuran lebih kecil, namun mempunyai massa yang lebih besar. Apalagi bila dibandingkan dengan lubang hitam pada kanan gambar yang mempunyai massa luar biasa besar. Fenomena tersebut sanggup dijelaskan oleh teori relativitas yang dinyatakan oleh Albert Einstein.

Gambar 1. Teori relativitas menjelaskan gravitasi sebagai hasil distorsi ruang.

Relativitas merupakan salah satu dari beberapa teori mengenai gerak, yang dirancang untuk menjelaskan penyimpangan dari mekanika Newton yang timbul akhir gerak relatif yang sangat cepat. Teori ini telah mengubah pandangan kita mengenai ruang, waktu, massa, energi, gerak, dan gravitasi. Teori ini terdiri atas teori khusus dan teori umum, yang keduanya bertumpu pada dasar matematika yang besar lengan berkuasa dan keduanya telah diuji dengan percobaan-percobaan dan pengamatan.

Teori khusus, yang dikembangkan oleh Einstein pada tahun 1905, berkenaan dengan pembandingan pengukuran yang dilakukan dalam kerangka contoh inersia berbeda yang bergerak dengan kecepatan konstan relatif satu sama lain. Di lain pihak, teori umum, yang dikemukakan tahun 1915, berkenaan dengan kerangka contoh dan gravitasi yang dipercepat. Pada cuilan ini pembahasan akan lebih terfokus pada teori fisika" target="_blank">relativitas khusus.

A. fisika" target="_blank">Relativitas Newton

Teori relativitas muncul dari kebutuhan terhadap kerangka acuan, yaitu suatu patokan yang sanggup dipakai ilmuwan untuk menganalisis aturan gerak. Pada waktu kelas X, kalian telah mempelajari Hukum Newton wacana gerak, di mana Hukum I Newton tidak membedakan antara partikel yang membisu dan partikel yang bergerak dengan kecepatan konstan. Jika tidak ada gaya luar yang bekerja, partikel tersebut akan tetap berada dalam keadaan awalnya, membisu atau bergerak dengan kecepatan awalnya.

Benda akan dikatakan bergerak apabila kedudukan benda tersebut berubah terhadap kerangka acuannya. Kerangka contoh di mana Hukum Newton berlaku disebut kerangka contoh inersia. Jika kita mempunyai dua kerangka contoh inersia yang bergerak dengan kecepatan konstan relatif terhadap yang lainnya, maka tidak sanggup ditentukan cuilan mana yang membisu dan cuilan mana yang bergerak atau keduanya bergerak. Hal ini merupakan konsep Relativitas Newton, yang menyatakan “gerak mutlak tidak sanggup dideteksi”.

Konsep ini dikenal oleh para ilmuwan pada kurun ke-17. Tetapi, pada selesai kurun ke-19 pemikiran ini berubah. Sejak dikala itu konsep relativitas Newton tidak berlaku lagi dan gerak mutlak dideteksi dengan prinsip pengukuran kecepatan cahaya.

B. Transformasi Galileo

Pada sudut pandang klasik atau Galileo, bila terdapat dua kerangka contoh S dan S′ yang masing-masing dicirikan dengan sumbu koordinat yang ditunjukkan Gambar 2. 

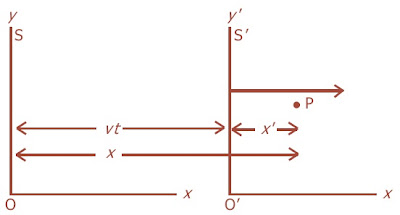Gambar 2. Kerangka contoh S bergerak ke kanan dengan kecepatan v relatif terhadap kerangka S.

Sumbu x dan x' saling berimpitan, dan diasumsikan kerangka S′ bergerak ke kanan (arah x) dengan kecepatan v relatif terhadap S. Untuk menyederhanakan, diasumsikan bahwa contoh O dan O' dari kedua kerangka contoh saling berimpit pada t = 0.

Sekarang, dimisalkan terjadi sesuatu di titik P yang dinyatakan dalam koordinat x ', y ', z' dalam kerangka contoh S' pada dikala t'. Bagaimana koordinat P di S? Perlu diketahui, sebab S dan S' mula-mula berimpitan, sehabis t, S' akan bergerak sejauh vt'. Sehingga pada dikala t ' akan berlaku:

x = x' + vt' ..................................................... (1)

y = y'.............................................................. (2)

z = z' ............................................................. (3)

t = t '.............................................................. (4)

Persamaan-persamaan tersebut dinamakan persamaan transformasi Galileo.

Jika titik P pada Gambar 10.2 menawarkan sebuah benda yang bergerak, maka komponen vektor kecepatannya di S' dimisalkan u_x', u_y', u_z'. Diperoleh ux' = Dx'/Dt', uy' = Dy' /Dt', dan u_z' = Dz' /Dt'. Jika pada t₁' partikel berada di x₁′ dan sesaat kemudian, t₂ berada di x₂′, diperoleh:

Jadi, kecepatan P ibarat terlihat dari S akan mempunyai komponen ux, uy, dan uz. Untuk komponen yang berafiliasi dengan komponen kecepatan di S' diperoleh:

Dapat disimpulkan bahwa:

u_x = u_x' + v ......................................................... (6)

u_y = u_y' ............................................................... (7)

u_z = u_z' ................................................................ (8)

yang disebut persamaan transformasi kecepatan Galileo.

Contoh Soal 1 :

Sebuah transformasi koordinat x' pada transformasi Galileo dinyatakan oleh x' = x – vt. Buktikan bahwa transformasi Galileo untuk kecepatan adalah u_x' = u_x' – v!

Penyelesaian:

Transformasi kecepatan, u_x' terhadap u_x dapat diperoleh bila tiap koordinat diturunkan terhadap peubah waktu t.

C. fisika" target="_blank">Percobaan Michelson Morley

D. fisika" target="_blank">Relativitas Einstein atau fisika" target="_blank">Postulat Einstein.

E. fisika" target="_blank">Massa Relativistik, fisika" target="_blank">Momentum Relativistik, dan fisika" target="_blank">Energi Relativistik.

Anda kini sudah mengetahui Relativitas Khusus dan Relativitas Newton. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.

Referensi :

Budiyanto, J. 2009. Fisika : Untuk SMA/MA Kelas XII. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 298.